Introduction

Bagging vs. Boosting

There are two reasons for errors in an estimator namely variance or bias.A too complex model(unpruned decision trees) have high variance but low bias whereas a too simple model( Weak learners like decision stumps ) have high bias but low variance.To minimize these two types of errors two different approaches are required namely bagging(complex models/high variance) and boosting(simple models/high bias).
In more general terms bagging also known as bootstrap aggregating tries to build complex models over many bootstrapped samples from the same distribution(datasets) and gives simpler but more robust model either by simple averaging or majority voting over former complex models.Whereas boosting is an approach of ensembling strong learners from weak learners simply by improving over the misclassified labels from dataset in a finite number of iterations.In this blog we will try to shed some light over the learning approach of boosting meta-algorithm .

AdaBoost

Weak Learners And Boosting

In 1988 Michael Kearns remarked whether one can boost a weak learner to a strong learner which was answered by a remarkable paper by Rob Schapire published in 1990. Thereby paving a way for a novel approach of utilizing the power of a weak learners two give a better , versatile and more robust strong learners.Yoav Freund and Robert Schapire came together to work on a much strong & refined meta-algorithm called AdaBoost or Adaptive Boosting which won them the prestigious Gödel Prize in 2003.But before we dive into realms of Adaboost algorithm we need to have a clear understanding of what a weak learner is.
By weak I mean that classifier does a better job at classifying than randomly guessing but not by much i.e. it classifies slightly better than 50% of the correct labels in the sampled outputs.A weak classifer could be a simple decision stump(A stump is a two-node tree, after a single split.), C4.5 and ID3 generated decision trees also perform well as weak learners for adaboost.

Algorithm

1. If there are N datum in the dataset then initially we distribute equal weights to all datapoints (wi=1/N).
   
2. We take M iterations from m=1 to M and for each m
   a) Fit a weak classifier to the training data using above weights.
   b) err is calculated as weighted average of mis-classified dataum
   c) alpha for each iteration is calculated. err must be less then 0.5 ,i.e. weak learners should be better than random guesses, for alpha>1.
   d) exp(Indicator function(I)) gives 1 when I=0 hence weight remain unchanged else when I=1 weight is readjusted(increases) to weight*alpha.
   
3. Now new classifier is weighted sum of on each M iterations' alpha value and classifier output.

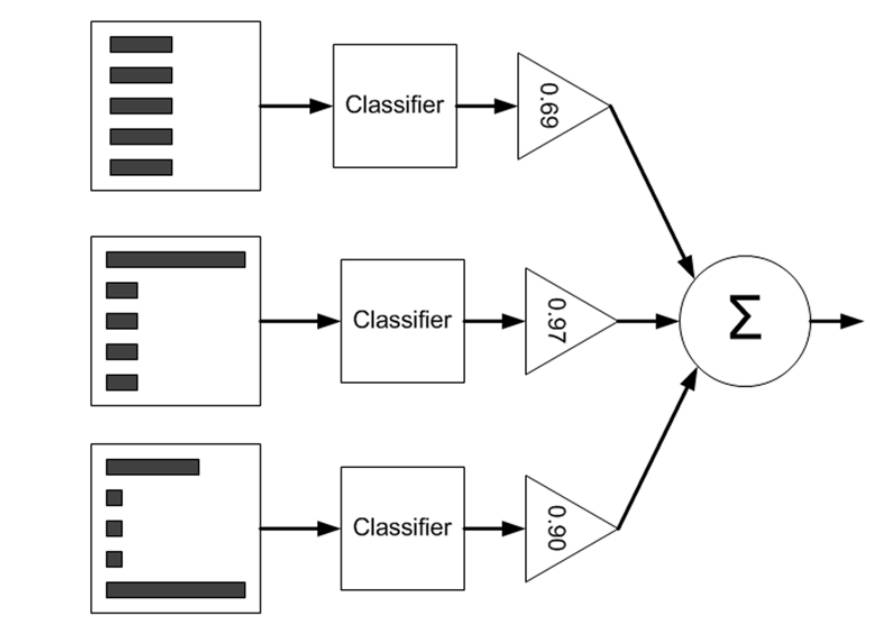Fig-2 Schematic representation of AdaBoost; with the dataset on the left side,the different widths of the bars represent weights applied to each instance. The weighted predictions pass through a classifier, which is then weighted by the triangles (alpha values). The weighted output of each triangle is summed up in the circle, which produces the final output. Source:MLIA-Peter Harrington