Randomforests And Bootstrap Aggregating

As we know in simple averaging methods RFs perform better than Bootstrap Aggregating or bagging by considerably reducing the high variance (see bias-variance tradeoff) of a single classifier by continuous independent sampling with replacement from the same distribution(dataset). This performance gain of RFs is described very well in this Leo Breiman(2001) paper and also in The Elements of Statistical Learning : Hastie,Tibshirani,Friedman in the section RandomForests.

I will briefly describe the idea of performance gain in Rfs over bagging here. Since in both the ensembling methods a single classifier(decision trees), which is very prone to high variance, when makes use of all the available features, it tends to over-fit since a more complex tree dependence structure is generated. Averaging over different classifiers, with low collinearity among them, decreases the over-all complexity of the final ensembled model. But including all the feature is not a good idea, since all the features might not help much in overall information gain for individual classifier and many a time can prove to be a source of noise. To overcome this problem L. Breiman proposed the idea of selecting features randomly from some fixed number of features..

Code

In the following code snippet, oob error is calculated for each estimator that is being added to the classifier grown on Boston_housing_data and a graph is plotted on matplotlib for the same.

Note : I have used sqrt(Number of features) as max_feature which is the recommended number of features to be sampled from the distribution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

from collections import OrderedDict
from sklearn.datasets import load_boston
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.datasets import make_classification


import matplotlib.pyplot as plt

RAND=123

# Generate a binary classification dataset.
boston = load_boston()
X= boston.data
#y= boston.target
y= np.array(boston.target).astype(str)


ensemble_clfs=[("RandomForestClassifier",RandomForestClassifier(warm_start=True, oob_score=True,
                               max_features="sqrt",
                               random_state=RAND)), 
               ("BaggingClassifier", BaggingClassifier(
                              oob_score=True,
                              random_state=RAND) 
               )
               
             ]

#initialize error rate dictionary 
error_rate = OrderedDict((label, []) for label, _ in ensemble_clfs)

#Required Params
max_est = 100
min_est = 10

for label,clf in ensemble_clfs:
    for i in range( min_est, max_est + 1 ):
        clf.set_params( n_estimators = i )
        clf.fit( X, y )
        #Out_of_bag Score(OOB score)
        oob_err=1-clf.oob_score_
        error_rate[label].append((i,oob_err))

#print oob_err_list vs ensemble classifier
for label,ensemble_err in error_rate.items():
        Xn_est,Yoob_err=zip(*ensemble_err)
        plt.plot(Xn_est,Yoob_err,label=label)    




plt.xlim(min_est, max_est)
plt.xlabel("n_estimators")
plt.ylabel("OOB error rate")
plt.legend(loc="upper right")
plt.show()

OOb_Score Vs n_estimators Plot

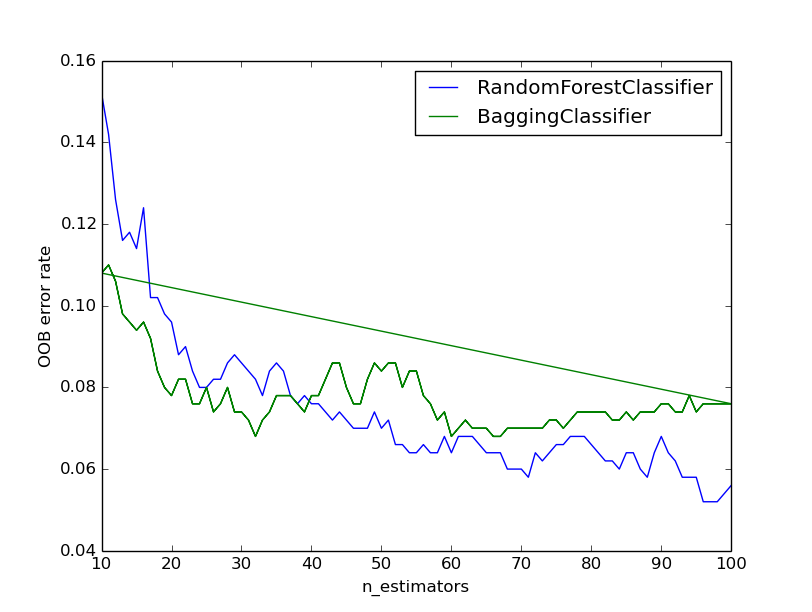
In the above plot we tried to plot out-of-bag error(error estimated over currently ensembled classifiers with data point not in dataset or out of the bag) on Y-axis and X-axis shows “n_estimator” which describes the number of estimator ensembled till now. As the number of estimator increase overall variance reduces for both the ensembling methods. But Random Forest is the clear winner all the way while growing the forest where #Tress equals 100. This shows how random feature selection generalizes the final model and reduces over-fitting and variance than choosing all the features.

Also remember,the performance of RFs is very much dependent upon the collinearity between the estimators being grown for the forests. Lesser the collinearity, better is the performance of the estimator.